
(from HP of School of Math., Univ. Southampton)
(注6)
時間・空間平均した方程式は、必然的に平均したことにより失われた微細構造の影響を表す項を含む。その項を評価するためには何らかのモデル化が必要であり、それを構成方程式と呼ぶ。
(注7)
ただし、複雑な混相流において相界面の運動と各相の支配方程式を厳密に連成させて計算することは、現在の計算機能力をもってしても不可能である。その場合、それらを時間・空間平均した方程式を解くことによりシミュレーションが行われている。
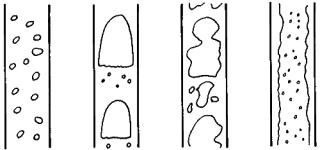
気泡流 スラグ流 チャーン流 環状噴霧流
(注6)
流れを各相が占める幾何的な様相によって分類したものを流動様式と呼ぶ。鉛直管内の気液二相流の場合は例えば下図に示すようなものが挙げられる。
(注5)
流れが流れ方向には変化せず流れを横切る1方向のみ変化する場合を平行流という。厳密な平行流はCuette流、Poiseuille流などの極端に単純な流れに限られ、物体後流、境界層などは厳密には平行流ではない(図2)。
(注4)
撹乱方程式のスペクトル解析において、作用素が非正規のとき一般にはその固有関数は互いに直交しない。その場合、固有値がすべて時間的に減衰する解に対応する場合でも、それらの固有関数の組み合わせによっては過渡的に代数的な増幅を示す場合がある。特に初期撹乱がある程度の大きさをもつとき、この代数的な過渡成長が乱流への遷移に影響を与える可能性が生じる。
(注3)
流れが不安定であるとき、そこに(時間・空間的に)局所的な微小撹乱を与えると、それは時間とともに増幅する。それが流れとともに移動していく場合を対流不安定、その場に留まる場合を絶対不安定と呼ぶ。
(注2)
固体、液体、気体などの互いに異なる状態もしくは互いに混じり合わない複数の物質(それぞれの状態・物質を相と呼ぶ)が混在する流れを混相流という。相の境界には界面が存在し、また温度や圧力の変化によって(固体から液体(融解)、液体から気体(沸騰)などの)相転移が生じるが、これらが流れと相互作用して非常に複雑な様相を示すことになる。ビールを注いだ時の流れ(気液二相流)、掃除機でゴミを吸い込む時の流れ(固気二相流)など身の回りにも混相流の例はいたるところに見られる。
O. Reynolds (1883)
Philos. Trans.
174, 935-982.
(注1)
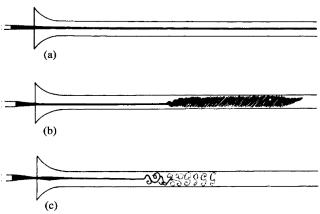
Osborne Reynoldsは(極力乱れが入り込まないように注意深く設定した)円管内の流れに染料を注入し、その様子を調べた(右図参照)。流速、管径、温度(粘性・密度)を変化させると、Reynolds数(=密度×流速×管径/粘性)と呼ばれる無次元数が十分小さいときには染料はきれいな直線を描く(右図(a))が、Reynolds数を徐々に増加させると、途中から乱れて染料が管内全体に広がるようになる(右図(b))ことが観測された。
これは、Reynolds数が大きくなると、直線状の整った流れ(層流)は不安定になり、乱れた流れ(乱流)に遷移するようになることを示している。





 O. Reynolds (1883) Philos. Trans. 174, 935-982.
O. Reynolds (1883) Philos. Trans. 174, 935-982.
